Le système métrique dans le Cantal par Jean-Baptiste Franiatte [vers 1800]
Jean-Baptiste Franiatte, expert géomètre de la ville d’Aurillac et commissaire pour les poids et mesures du département du Cantal, est à l’origine d’une des premières tentatives de réalisation d’un tableau de concordance entre les anciennes mesures héritées de l’Ancien Régime et le système métrique mis en place par la Révolution. En 1789, il n’existe aucun système de mesure unifié entre les diverses régions de France. L’étalonnage des poids et mesures est alors octroyé au roi, et on dénombre dans le royaume plus de 800 unités de mesure différentes. Certaines sont liées à la morphologie du corps (pouce, doigt, poignée, brassée, pied, pas), d’autres au travail (hommée, fauchée, journal), d’autres encore au transport (ânée, charge, sac, tonneau). La complexité vient aussi de ce qu’une même dénomination, le pied, par exemple, correspond à une vingtaine de longueurs différentes selon les lieux et les corps de métier. Ainsi dans le Cantal, pour les mesures agraires, on utilise la sétérée, le journal ou la cartelée, mais tandis que la sétérée d’Aurillac vaut 17,83 ares (ou 1783 m2), celle de Maurs vaut 32,10 ares (ou 3210 m2). Et il en va de même pour l’ensemble des unités de mesure de distance, de longueur, de surface ou de poids. Une même dénomination peut recouvrir des réalités très différentes selon les localités.
Un tel système, source de confusions et d’embarras, constitue une entrave au commerce et à l’industrie dont l’essor réclame un système unifié. Sous l’Ancien Régime, plusieurs tentatives de simplification et d’uniformisation avaient déjà été faites, malheureusement sans succès, et la réforme des poids et mesures reste une des revendications les plus fréquemment exprimées dans les cahiers de doléances. « Un roi, une loi ; un poids et une mesure » est bien une des doléances inscrites à l’ordre des États généraux de 1789. L’abolition des privilèges ouvre la voie à une réforme enfin possible. Le roi n’étant plus à l’origine de l’étalonnage, il s’agit de trouver dans la nature « une mesure universelle et invariable, reproductible et vérifiable partout et toujours » (Talleyrand). Le 26 mars 1791, le choix du quart du méridien terrestre comme unité universelle et naturelle est fait sur la recommandation de Condorcet et de l’Académie des sciences, car cette mesure « ne renferme rien ni d'arbitraire, ni de particulier à la situation d'aucun peuple sur le globe ». La naissance du mètre – dont la longueur est établie comme « égale à la dix millionième partie du quart du méridien terrestre » – est officialisée par le décret du 1er août 1793, « qui établit pour toute la République la même uniformité dans les poids et mesures ». Ce premier décret est complété par celui du 18 germinal an III (7 avril 1795) qui institue le système métrique décimal. Il s’agit d’une véritable révolution dans le calcul des surfaces et des volumes. L’unité de mesure de base étant déterminée, il suffit désormais d’établir toutes les unités de mesure qui en découlent : le mètre carré, le mètre cube, le litre, le gramme… Ce décret supprime et interdit toute autre unité de mesure. Toutefois, on imagine aisément que la mise en pratique du système métrique n’a pu se faire en quelques mois ou même quelques années. Il est impossible d’abolir des siècles de pratiques et d’habitudes en si peu de temps. A l’heure de l’euro, certains de nos compatriotes parlent toujours en anciens francs alors qu’ils n’ont plus cours depuis plus de 60 ans ! Ce document n’est pas daté mais il est dit « présenté au citoyen Riou Préfet du Cantal ». Il s’agit du premier préfet du Cantal en poste depuis le 11 ventôse an VIII (2 mars 1800). On sait aussi que le même Franiatte est l’auteur du Tableaux des anciens poids et mesures en usage dans la ci-devant Haute-Auvergne comparés aux poids et mesures du nouveau système métrique publié en 1802. On peut donc raisonnablement dater ce document de la période 1800-1801, soit près de 5 ans après l’interdiction des anciennes unités de mesure.
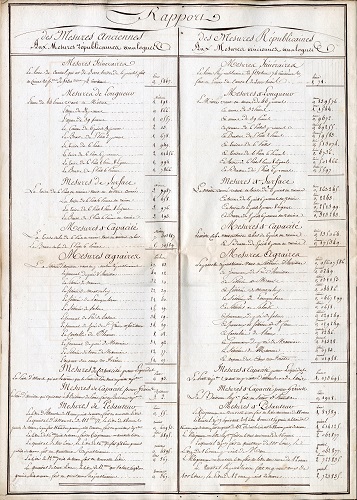
Par son travail, Jean-Baptiste Franiatte fait œuvre de vulgarisation. Il se propose de donner « un rapport réciproque des mesures anciennes et nouvelles, avec différents moyens de les comparer les unes aux autres ». Les unités de mesure ne portent pas encore toutes les dénominations actuelles. Il utilise le mètre, le mètre carré et le mètre cube, le kilogramme ou « nouvelle livre » mais aussi la « lieue républicaine », la « perche républicaine » ou encore la pinte et le boisseau. Mais là n’est pas l’essentiel, la véritable révolution est qu’il s’agit bien désormais d’un système décimal unifié. Franiatte établit un tableau de concordance entre toutes les mesures dites « anciennes » et les mesures dites « républicaines ». L’aune de 44 pouces, mesure de longueur utilisée dans le canton d’Aurillac, vaut désormais 1,191 mètres et à l’inverse le mètre vaut 0,839576 aunes de 44 pouces. Pour bien se faire comprendre, il donne en exemples plusieurs cas pratiques de conversion : « On demande combien font 100 mètres linaires en aune de 44 pouces. Multipliez par 100 le nombre 0,839576 (rapport du mètre à l’aune). Séparez ensuite les six derniers chiffres vers la droite par une virgule, parce que le multiplicande a six décimales, et vous trouverez que le résultat de la multiplication donne 83 aunes 957600, c'est-à-dire 83 aunes 96 centièmes en négligeant les quatre derniers chiffres et en augmentant d’une unité la décimale précédente ». Pour Jean-Baptiste Franiatte c’est un « moyen simple de convertir en fractions anciennes, les fractions décimales ». Autre exemple « Le kilogramme ou livre républicaine fait en livres anciennes de 16 onces, 2,042877 livres. Si l’on veut savoir combien d’onces font ces fractions décimales, on les multiplie par 16 et l’on trouve 0,686032 once. Ces fractions ne contenant pas d’onces, comme l’on voit, on cherche combien de gros elles contiennent, et l’once étant composé de 8 gros, on les multiplie par 8 qui donnent 5,488256 gros : il faut multiplier les fractions décimales des gros pour trouver combien de grains elles contiennent, et le gros étant composé de 72 grains, l’on multipliera 488256 par 72, pour trouver 25,154432 grains. Par conséquent le kilogramme ou nouvelle livre vaut 2 livres 5 gros 35 grains 15 centièmes de grain » et tout cela sans calculatrice ! Je vous laisse seuls juges de la simplicité du procédé.
Cotes ADC : 3 Z 16
Document rédigé par Nicolas Laparra
Sources : Christiane DOUYÈRE-DEMEULENAERE, « Le système métrique décimal », Histoire par l'image [en ligne], consulté le 20 avril 2022. URL : http://histoire-image.org/fr/etudes/systeme-metrique-decimal